
하이어라키컬 클러스터링은 기본적으로
K-means와 유사하다

이러한 데이터가 있을때


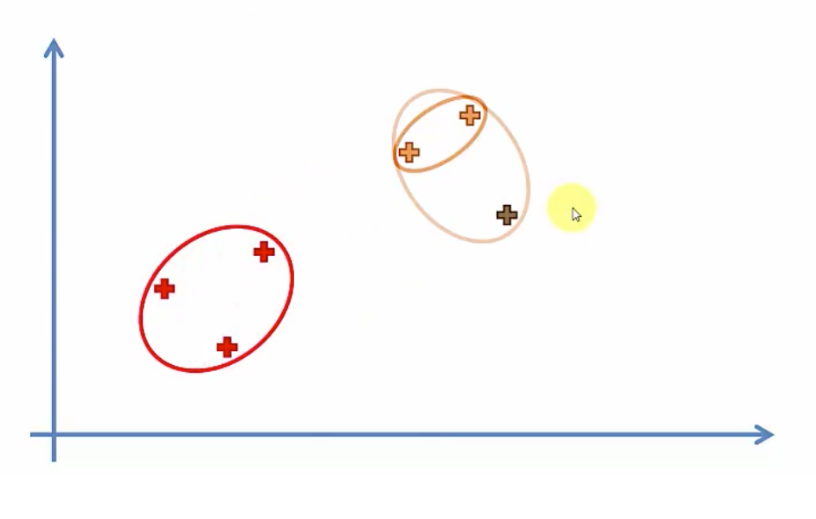

한 그룹 한그룹씩 묶어 나가면서 마지막에 하나의 그룹이 될때까지 그룹화를 한다

클러스터로 묶는 기준은 어떤 점에 중점을 두느냐에 따라 다르다
Dendrogram
그래서 이 방법을 덴드로그램으로 표현하는데




위 그림처럼 한 그룹이 지어질때마다
그 거리를 y축으로 표현하여 묶어주다가
한 그룹으로 묶어진 뒤에
사람이 멀어지는 거리를 보고
몇개의 그룹으로 나눌것인지 판단하는 시스템이다
아래에있는 묶음들은 거리가 가까워서 짧지만 마지막에 묶이는 2그룹은
거리가 멀기때문에 길게 나타난다
보통 그 곳을 잘라 두 그룹으로 나타낼 수 있겠다
import scipy.cluster.hierarchy as sch
sch.dendrogram( sch.linkage(X , method= 'ward') )
plt.title('Dendrogram')
plt.xlabel('Customers')
plt.ylabel('Distances')
plt.savefig('dendrogram.png')
plt.show()
method= 는 그룹화할때 기준을 어떻게 할 것이냐 라는 뜻이며 ward가 제일 일반적

이렇게 표시가 가능하겠다
from sklearn.cluster import AgglomerativeClustering
AgglomerativeClustering 는 병합적군집이라는 뜻
hc = AgglomerativeClustering(n_clusters = 6 )
y_pred = hc.fit_predict(X)
df['Group'] = y_pred
이렇게 그룹화가 가능하다
K-Means와의 차이점
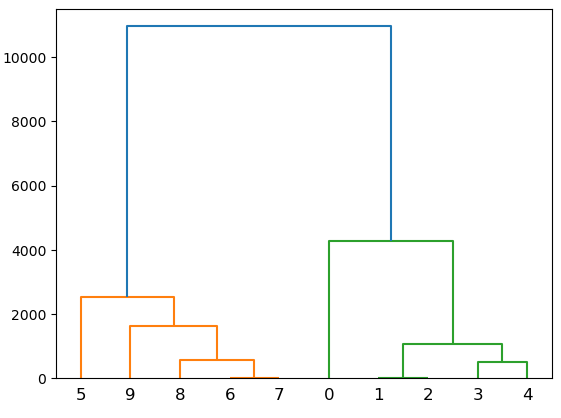
이런 덴드로그램을 보고 2로 그룹을 지었을때와
from sklearn.cluster import AgglomerativeClustering
hc = AgglomerativeClustering(n_clusters=2)
y_pred = hc.fit_predict(X)
df['Group']= y_pred
이번엔 K-Means와 비교해보자
from sklearn.cluster import KMeans
wcss = []
for i in range(1, 5+1):
kmeans = KMeans(n_clusters= i , random_state= 5)
kmeans.fit(X)
wcss.append( kmeans.inertia_ ) wcss
[74525310.2, 14500293.600000001, 5387740.75, 2187714.5, 854349.4166666667]plt.plot( range(1,5+1) , wcss)
plt.show()

K-means에서도 2그룹을 지었을때가 크게 달라진다
kmeans = KMeans(n_clusters=2, random_state=5)
y_pred2 = kmeans.fit_predict(X)
df['Group2'] = y_pred2

데이터가 적어서 그럴진 몰라도 같은 그룹으로 지어진것을 볼 수 있다
데이터가 수십만개 수백만개라면 조금씩 조금씩 다를 수도 있겠지만
데이터가 적다면 K-means와는 크게 차이가 없다
'Python > MachineLearning' 카테고리의 다른 글
| Time Series Data forecasting Prophet (0) | 2024.04.19 |
|---|---|
| K-Means Clustering - 개념 + WCSS (0) | 2024.04.15 |
| Decision Tree 의사결정 트리 - 개념 (0) | 2024.04.15 |
| Support Vector Machine - 개념 (0) | 2024.04.15 |
| K - Nearest Neighbor - 개념 (0) | 2024.04.15 |



