
Linear Regression 에서는
각종 데이터들 사이에서
어떤 값이 나올지 예측 하는거였다면
Logistic Regression은 조금 다르다
로지스틱리그레션은은 답이 0과 1 뿐이며
0일지 1일지 확률을 따지는것 뿐이다


평균값에 가까워지기 위해 변형된것인데
기존의 리니어 리그레션 에서 조금 달라지는 모습이 필요하다
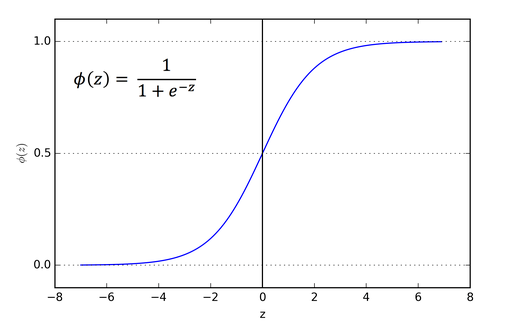
비슷한 함수의 이름은 sigmoid function
이 시그모이드를 대입하여 일차방정식으로 만드는 것이다
그리하여

0 과 1뿐인 선택지의 확률을 알 수 있게 된다( p 는 확률)

물론 0.5를 기준으로 나뉘어 지게 되지만 0.1, 0.8 같은 값은 충분히 납득이 갈 수치다
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression()
LogisticRegression은 classifier 라고 이름 지어주자
classifier.fit(X_train,y_train)
classifier.predict(X_test)
array([0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1,
1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0,
1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1,
0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0,
0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0], dtype=int64)
기존의 리니어 레그리션과 같이 예측을 하면 되며
추가로
classifier.predict_proba(X_test)

각각의 확률을 알 수 있다
[ a , b ] 라고 했을때 a가 0인 확률, b가 1인 확률
이렇게 했을때 우리는 아직 눈으로 봐서
이게 얼마나 맞았는지 틀렸는지
0을 1로 틀렸는지
1을 0으로 틀렸는지
0이 맞았는지
1이 맞았는지
자세히 알지 못한다
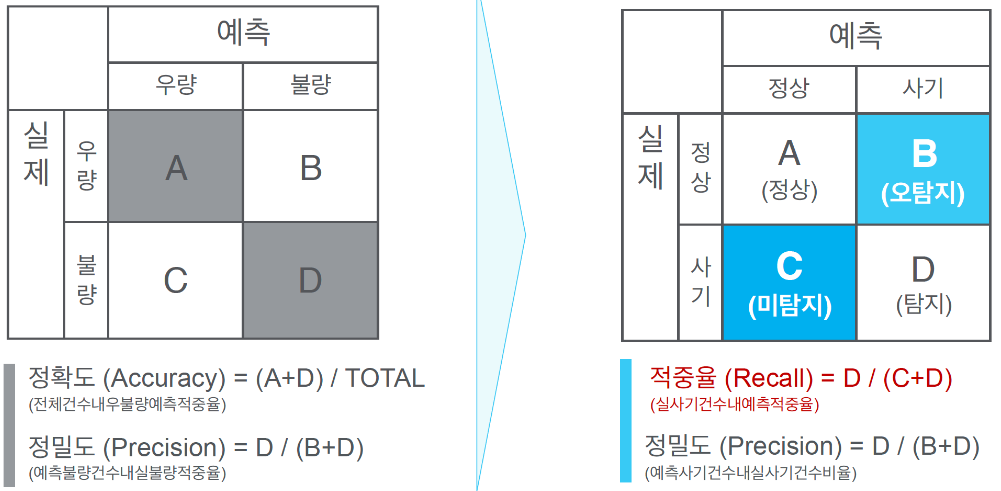
이렇게 봐야 알기 편하다
이것을 Confusion Matrix 라고 하며 분류 결과표 라고 한다
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
알아보기 전에 임포트를 먼저 해준다
cm = confusion_matrix(y_test, y_pred)
cm
array([[52, 6],
[14, 28]], dtype=int64)
이렇게 알려주며
정확도는
accuracy_score(y_test, y_pred)0.8
이렇게 알아 볼 수 있다
from sklearn.metrics import classification_report
classification_report(y_test, y_pred)
' precision recall f1-score support\n\n 0 0.79 0.90 0.84 58\n 1 0.82 0.67 0.74 42\n\n accuracy 0.80 100\n macro avg 0.81 0.78 0.79 100\nweighted avg 0.80 0.80 0.80 100\n'
그리고 classification_report는 평가지표를 출력해주며
Precision은 정밀도를 뜻하며 예측한 클래스중 실제로 해당 클래스인 데이터의 비율
Recall은 재현율을 뜻하며 실제 클래스중 예측한 클래스와 일치한 데이터의 비율
F1-score는 정밀도와 재현율의 조화 평균
Support는 각 클래스의 실제 데이터 수를 뜻 한다
그리고 시각화는 히트맵을 사용하여 볼 수 있다
import seaborn as sb
sb.heatmap(data = cm , cmap = 'OrRd', annot=True)
plt.show()

'Python > MachineLearning' 카테고리의 다른 글
| Support Vector Machine - 개념 (0) | 2024.04.15 |
|---|---|
| K - Nearest Neighbor - 개념 (0) | 2024.04.15 |
| Regression 4) 인공지능 저장 및 사용 (0) | 2024.04.13 |
| Regression 3) New 데이터의 예측값은? (1) | 2024.04.13 |
| Regression 2) Error, MSE, RMSE (0) | 2024.04.13 |

